完全二分木はこういうやつです。
最下層以外の全部の層がノードで埋められ、最下層のnodeは左に詰められているような二分木です(別の定義もある)。
完全二分木では配列を使って木を管理できることが知られています。具体的には
- 0-indexed
rootは0
node \(\ i\)の親、左の子、右の子はそれぞれ\(\ (i-1)/2,\,2i+1,\,2i+2\) - 1-indexed
rootは1
node \(\ i\)の親、左の子、右の子はそれぞれ\(\ i/2,\,2i,\,2i+1\)
割り算は切り捨てです。
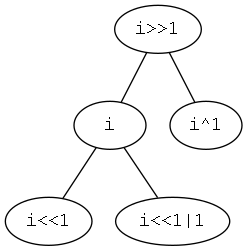
このふたつは同じように見えて実装上少し違います。1-indexedはすべての演算をbit演算に置き換えることができるからです。つまり\(\ i\)に対して
#親
i>>1
#左の子
i<<1
#右の子
i<<1|1 一般にbit演算のほうがはやいので、速度が要求されるときは1-indexedにしたほうがいいでしょう。
ためしに計算してみると
import time
import numpy as np
np.random.seed(0)
A = np.random.randint(1, 10**8, 10**8)
# 0-indexed
time_memo = time.time()
for i in A:
work = (i - 1) // 2, 2 * i + 1, 2 * i + 2
print(f"{time.time()-time_memo} sec")
# 1-indexed
time_memo = time.time()
for i in A:
work = i >> 1, i << 1, i << 1 | 1
print(f"{time.time()-time_memo} sec")
53.23937201499939 sec
37.52551341056824 secとなり、1-indexedのほうがそこそこ速いです。
私はもともと0-indexedにこだわっていたんですが、0-indexedで実装したセグメント木で以下の問題を解いたときにTLEして、1-indexedにしたら間に合うということが起きたので、1-indexed派になりました。
0-indexedにこだわるのもよくないので1-indexedにしましょう!
姉妹へのアクセス
また0-indexedでできなくて1-indexedではできることがひとつあります。それが姉妹へのアクセスです。姉妹というのは同じ親をもつもう片割れのnodeのことです。1-indexedで自分が\(\ i\)のとき、姉妹へのアクセスは以下のようにできます。
#姉妹
i^1 この演算は\(\ i\)の1ケタ目だけをひっくり返す操作になっており、1-indexedでは左右の子の間でケタ上がりがないため、この操作が左右を行き来することに対応しています(左が偶数右が奇数なのがポイント)。
一方で0-indexedでは、左右の子の間でケタ上がりが起きるためこのような簡単な記述はできません
なので姉妹へのアクセスが必要なときなどはさらに1-indexedが優位になりますね。
まとめるとこんな感じ

コメント